lecture 24: Derivatives in Real Life and Optimization Problems

Real-Life Interpretations of Derivatives

1. Derivatives as Rate of Change

• The derivative of a function tells us how fast something is changing.
• Examples:
  • Velocity is the derivative of position.
  • Growth rate is the derivative of population.
  • Marginal cost/revenue is the derivative of cost/revenue.

Example: If $C(x)$ is the cost to produce $x$ units, then $C'(x)$ is the cost of producing one more unit (marginal cost).

Optimization with Derivatives

Optimization means finding:

• Maximum or minimum values
• Of a function that represents cost, area, revenue, volume, etc.

General Strategy

1. Identify the quantity to maximize or minimize.
2. Write it as a function of one variable.
3. Find the domain (possible values).
4. Compute the derivative and find critical points:
   • Where $f'(x) = 0$ or $f'(x)$ is undefined.
5. Determine if the point is a maximum or minimum using close values.
6. Interpret the result in the real-world context.

What does it mean to have the derivative be 0?

• If $f'(x) = 0$, then $f(x)$ is not changing at $x$, basically it's a turning point.
• This means $f(x)$ is at a local maximum or minimum.

In general, when $f'(x) > 0$, it means that the rate of change is positive, so the function is increasing.

When $f'(x) < 0$, it means that the rate of change is negative, so the function is decreasing.

Therefore, if $f'(x)$ switches from positive to negative, then $f(x)$ has a local maximum (was increasing, now decreasing). If $f'(x)$ switches from negative to positive, then $f(x)$ has a local minimum (was decreasing, now increasing).

Example: If $f(x) = x^2$, then $f'(x) = 2x$.
When $x > 0$, $f'(x) > 0$, so $f(x)$ is increasing.
When $x < 0$, $f'(x) < 0$, so $f(x)$ is decreasing.
Therefore, $f(x)$ has a local minimum at $x = 0$ since $f'(0) = 0$.

Application 1: Fence Optimization

Problem:

A farmer has 100 meters of fencing and wants to enclose a rectangular area. What is the largest area they can enclose?

Step-by-step:

• Let width = $x$, then length = $(50 - x)$ (since the perimeter is $2x + 2(50 - x) = 100$)
• Area: $A(x) = x(50 - x) = 50x - x^2$
• Derivative: $A'(x) = 50 - 2x$
• Set $A'(x) = 0 \implies x = 25$
• Compute close values: $A(24) = 480$, $A(25) = 625$, $A(26) = 552 \implies$ max at $x = 25$
  ($A(25) > A(24)$ and $A(25) > A(26)$, so it's a local maximum)

Max Area = $25 \times 25 = 625$ m$^2$

Application 2: Factory Production

Problem:

Suppose profit is modeled by:

$$P(x) = -2x^2 + 40x - 100$$

where $x$ is the number of items produced.

What is the optimal number of items to produce to maximize profit?

Steps:

• Find $P'(x) = \frac{d}{dx}[-2x^2 + 40x - 100] = -4x + 40$
• Set $P'(x) = 0 \implies x = 10$
• Compute close values: $P(9) = 98$, $P(10) = 100$, $P(11) = 98 \implies$ max at $x = 10$
  ($P(10) > P(9)$ and $P(10) > P(11)$, so it's a local maximum)

Optimal production: 10 units
Max profit: $P(10) = -2(10)^2 + 40(10) - 100 = 100$

Exercises

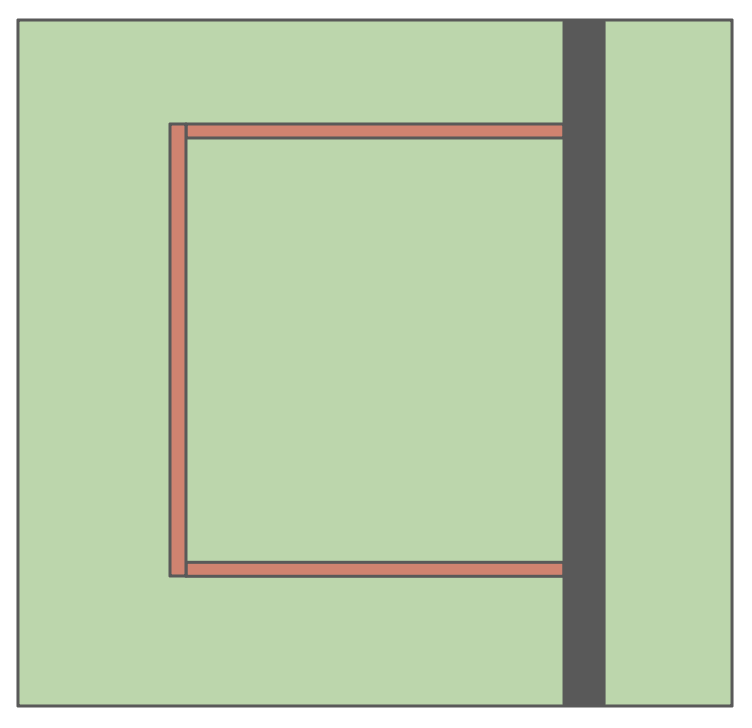
1. Fence Problem

A rectangular garden is to be enclosed on three sides with fencing (no fence along one side). You have 80 meters of fencing. What dimensions give the maximum area?

2. Profit Optimization

The cost of producing $x$ items is $C(x) = 5x + 16$ and revenue is $R(x) = 20x - x^2$. Find the number of items that maximizes profit.

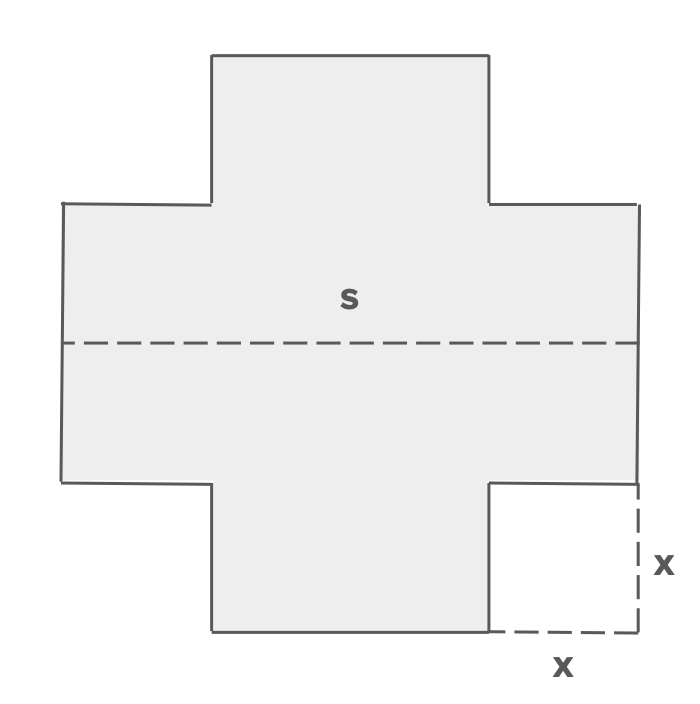
3. Box Volume Problem

A square sheet of metal with side length $s=30$ cm is folded into an open-top box by cutting equal squares from each corner. Write a function for the volume and find the optimal cut that maximizes the volume.

4. Cost Minimization

You want to design a can that holds 355 mL of soda. What radius and height minimize the surface area (cost of material)?

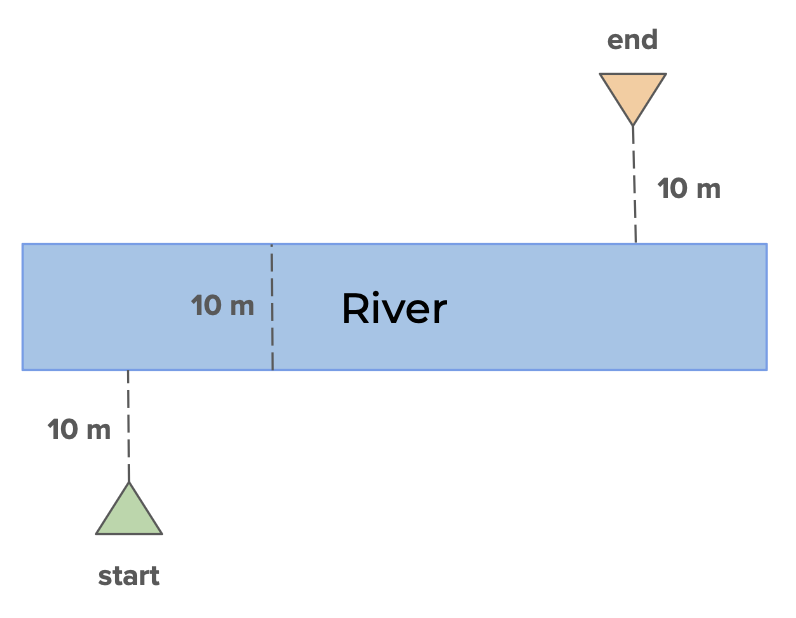
5. Time of Travel

You are trying to cross a river and walk to a point downstream. You can swim at 2 m/s and walk at 5 m/s. If the horizontal distance between the start and end points is 40 m, what path gets you there fastest?