Trigonometric functions and the unit circle

The unit circle

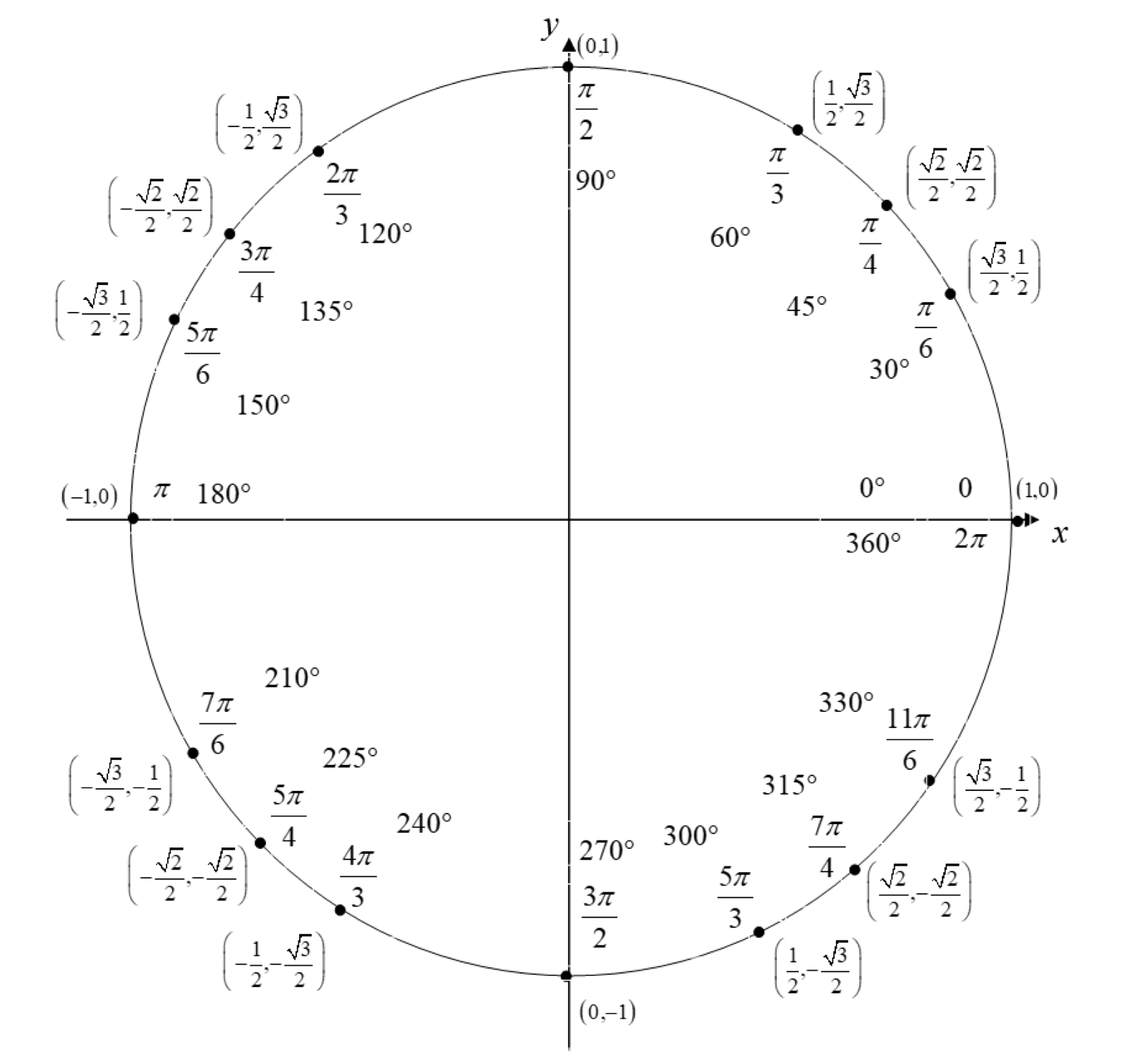
The unit circle is a circle with radius 1 centered at the origin (0,0) in the coordinate plane. It's fundamental to understanding trigonometric functions $sin(x)$ and $cos(x)$.

Interactive Unit Circle Visualization

ASTC rule

The ASTC rule is an acronym for remembering the positive signs of the trigonometric functions in each quadrant of the unit circle.

• A: All
• S: Sine
• T: Tangent
• C: Cosine

Sine and cosine

Trigonometry cheat sheet: link

The sine and cosine functions are defined as the y and x coordinates of a point on the unit circle, respectively.

We also define the tangent function as the ratio of sine and cosine:

$$\tan(x) = \frac{\sin(x)}{\cos(x)}$$

Properties of sine and cosine

• Domain: all real numbers.
• Range: $[-1, 1]$

1. They are periodic with period $2\pi$. ($sin(x + 2\pi) = sin(x)$ and $cos(x + 2\pi) = cos(x)$)
2. They are bounded between -1 and 1.
3. They are continuous.
4. $\sin(x) = \cos(\frac{\pi}{2} - x)$
5. $\cos(x) = \sin(\frac{\pi}{2} - x)$

Graphs

The graphs of the sine and cosine functions are shown below.

Pythagorean identity

$$\sin^2(x) + \cos^2(x) = 1$$

Common values

(image source: link)

Exercises

1. Basic trigonometric function values

2. ASTC rule and quadrant identification

3. Graphical analysis

Using the interactive unit circle above or graphing software:

a) For what values of $x$ in $[0, 2\pi]$ is $\sin(x) = \cos(x)$?

b) For what values of $x$ in $[0, 2\pi]$ is $\sin(x) = -\frac{1}{2}$?

c) For what values of $x$ in $[0, 2\pi]$ is $\cos(x) = \frac{\sqrt{3}}{2}$?

d) What is the maximum value of $\sin(x) + \cos(x)$ for $x$ in $[0, 2\pi]$?

4. Pythagorean identity practice

5. Periodicity and symmetry

6. Challenge exercises

1. $$\lim_{x \to 0} \frac{\sin(x)}{x}$$

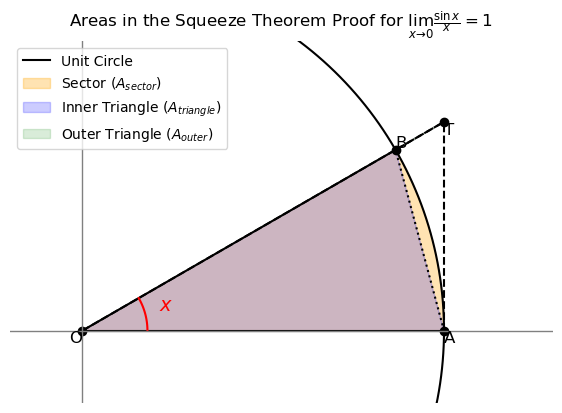
Solution using squeeze theorem:
consider the unit circle, we have the following areas:

1. Triangle area: $A_{triangle} = \frac{1}{2} \sin(x) \cos(x)$
2. Sector area: $A_{sector} = \frac{x}{2}$, since the area of a sector is $\frac{x}{2\pi} \pi r^2 = \frac{x}{2}$ for $r=1$.
3. Outer triangle area: $A_{outer} = \frac{1}{2} \tan(x) = \frac{1}{2} \frac{\sin(x)}{\cos(x)}$

We have $A_{triangle} \leq A_{sector} \leq A_{outer}$, therefore we have $\frac{\sin(x)\cos(x)}{2} \leq \frac{x}{2} \leq \frac{\sin(x)}{2\cos(x)}$.
Equivalently, we have $\cos(x) \leq \frac{x}{\sin(x)} \leq \frac{1}{\cos(x)}$.
Therefore, we have $\frac{1}{\cos(x)} \leq \frac{\sin(x)}{x} \leq \cos(x)$.

$$\lim_{x \to 0} \frac{1}{\cos(x)} = 1 = \lim_{x \to 0} \cos(x)$$

By squeeze theorem, we have $\lim_{x \to 0} \frac{\sin(x)}{x} = 1$.

2. $$\lim_{x \to 0} x \sin(\frac{1}{x})$$

3. $$\lim_{x \to 0} \frac{\tan(x)}{x}$$

4. $$\lim_{x \to 0} \frac{\sin(5x)}{x}$$