Review Questions

1. Given: $3\cdot 2^{a+1}\cdot 8^b - 10 = 2$, find $a+3b$.

2. Evaluate $4^{\log_2(5)} + \log_{11}(11^{4}) + 20^{\, \log_{20}(2005)}$ (Hint: world cup)

3. Solve for $x$: $\log (x^2) + \log (\frac{1}{x}) = 3$

4. Find the domain and range of the function $f(x)=2-\sqrt{9-3x}$.

5. Consider the functions $f(x)=\log_3(x-1)$ and $g(x)=\sqrt{2x-4}$.
   a. What are the domains of $f(x)$ and $g(x)$?
   b. Find $f(g(x))$ and $g(f(x))$.
   c. Find the domains of $f(g(x))$ and $g(f(x))$.

6. If the graph of the function $f(x)=1-\sqrt{x-1}$ is reflected across the y-axis, then shifted 2 units to the right and 3 units upward, then find the equation for the new graph.

7. If $f(x)=\sqrt{3x+4}$ and $g(x)=\frac{1}{x-4}$, what is the formula for $g^{-1}(f(x))$ and what is its domain?

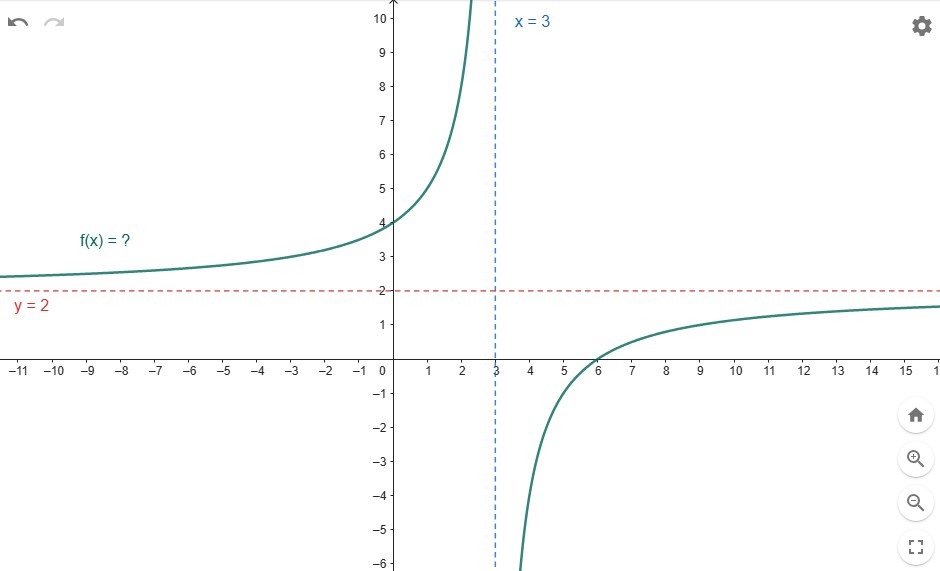
8. Let the function drawn in the graph below be $g(x)$, describe a formula for $g(x)$ in terms of $f(x)=x^2$. (Hint: think about function transformations)

9. Give a formula for the function drawn in the graph below.