lecture 7: Exponential and Logarithmic Functions — Graphs, Domain and Range, Discontinuities, and Infinity Behavior

Exponential Functions

1. What Is an Exponential Function?

An exponential function has the form:

$$f(x) = a^x$$

Where:

• $a > 0$ and $a \neq 1$
• $x$ is any real number

Example: $f(x) = 2^x$, $f(x) = 10^x$, $f(x) = e^x$

2. Real-World Examples

• Bacteria growth: population doubles every hour
• Finance: compound interest over time
• Physics: radioactive decay

These all grow (or decay) exponentially — very fast!

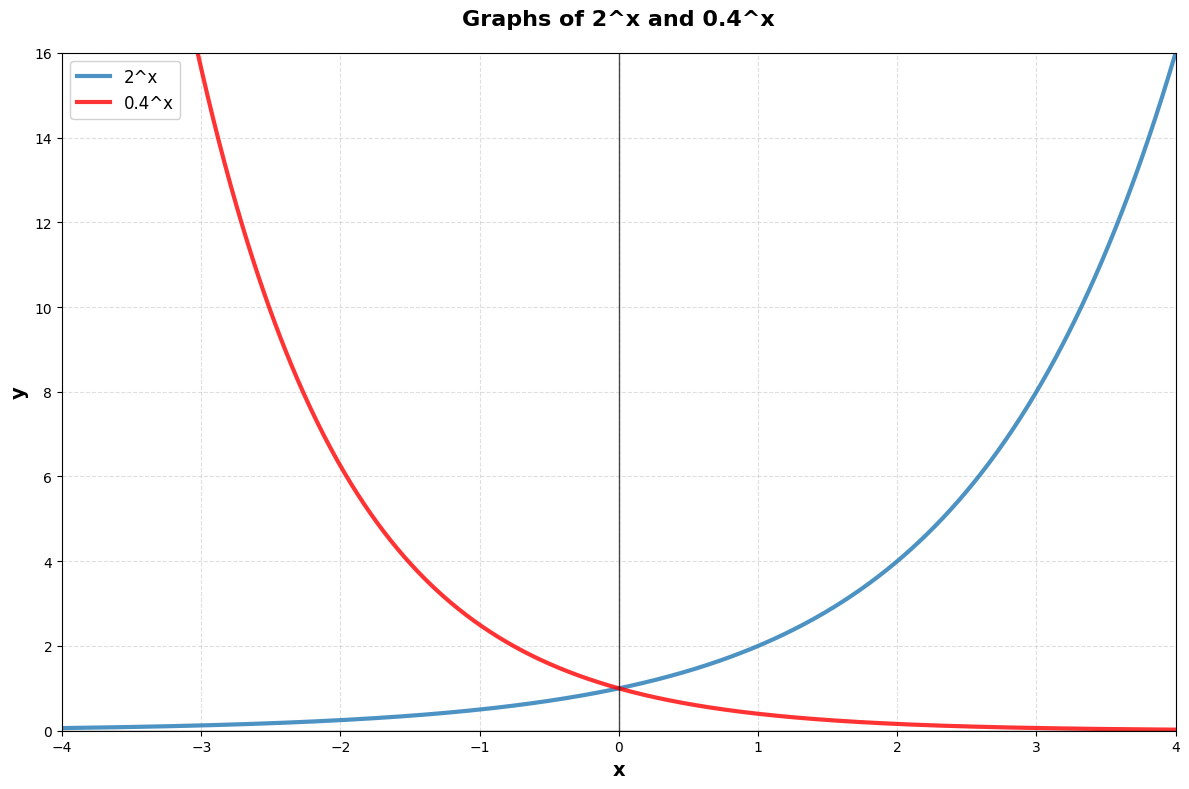
3. Graph and Behavior

Horizontal asymptote at $y = 0$

Graph of $2^x$ and $0.4^x$

Logarithmic Functions

1. What Is a Logarithm?

A logarithm is the inverse of an exponential function.

$$\log_b(x) = y \iff b^y = x$$

• $b > 0$, $b \neq 1$
• Most common: $\log_{10}(x)$, $\log_{2}(x)$, and $\ln(x)$ (natural log, base $e$)

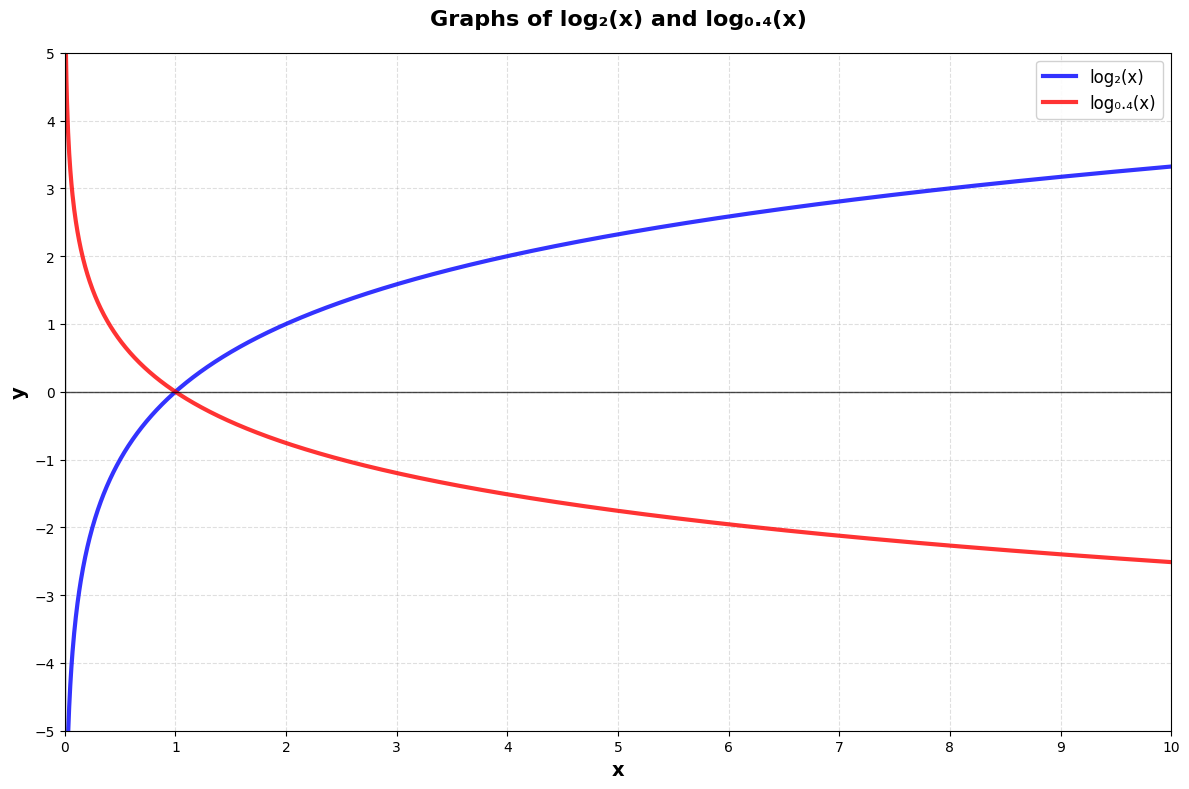
2. Graph and Behavior

No output for $x \leq 0$

Graph of $\log_2(x)$ and $\log_{0.4}(x)$

Domain and Range Summary

Infinity Behavior

Exponential Growth

• If $a > 1$:
  $f(x) = a^x \to \infty$ as $x \to \infty$,
  $f(x) \to 0$ as $x \to -\infty$

Exponential Decay

• If $0 < a < 1$:
  $f(x) \to 0$ as $x \to \infty$,
  $f(x) \to \infty$ as $x \to -\infty$

Logarithmic Behavior

$f(x) = \log_b(x)$

• If $b > 1$:
  $f(x) \to \infty$ as $x \to \infty$
  $f(x) \to -\infty$ as $x \to 0^+$

• If $0 < b < 1$:
  $f(x) \to -\infty$ as $x \to \infty$
  $f(x) \to \infty$ as $x \to 0^+$

Discontinuities and Asymptotes

1. Exponential Functions

• No discontinuities
• Horizontal asymptote: $y = 0$
• Smooth and continuous everywhere

2. Logarithmic Functions

• Essential discontinuity (vertical asymptote) at $x = 0$
• Not defined for $x \leq 0$
• No removable discontinuities

Logarithmic Properties

All rules and properties are valid for any base $b > 0$ and $b \neq 1$, and can be proven using the definition of logarithms ($b^y = x \iff \log_b(x) = y$).

• $\log_b(1) = 0$
• $\log_b(b) = 1$
• $\log_b(b^x) = x$
• $b^{\log_b(x)} = x$

Rules of logarithms:

• $\log_b(xy) = \log_b(x) + \log_b(y)$
• $\log_b(x/y) = \log_b(x) - \log_b(y)$
• $\log_b(x^k) = k \log_b(x)$

Change of base formula:

• $\log_b(x) = \frac{\log_k(x)}{\log_k(b)}$

Regular Exercises

1. Calculate the following

2. Domain and Range Practice

Determine the domain and range of each:

• a) $f(x) = 3^{x^2-4}$
• b) $f(x) = \log_{10}(x^2 - 1)$
• c) $f(x) = \log_{10}(2 - x)$

Solution
a) $( f(x) = 3^{x^2 - 4} )$

• Exponential functions are always defined for all real numbers.
• So, domain: $( \mathbb{R} )$
• The base 3 raised to any power is always positive, so the output is always greater than 0.
• Range: $( (0, \infty) )$

b) $( f(x) = \log_{10}(x^2 - 1) )$

• Logarithms are only defined for positive inputs.
• So:

$$x^2 - 1 > 0 \Rightarrow x^2 > 1 \Rightarrow x < -1 \text{ or } x > 1$$

• Domain: $(-\infty, -1) \cup (1, \infty)$
• Since $( x^2 - 1 )$ can get very large or very small positive values, the output (log) can be any real number.
• Range: $( \mathbb{R} )$

c) $f(x) = \log_{10}(2 - x)$

• Require: $2 - x > 0 \Rightarrow x < 2$
• Domain: $( (-\infty, 2) )$
• As $x \to -\infty$, $2 - x \to \infty$, so $\log_{10}(2 - x) \to \infty$
• As $x \to 2^-$, $2 - x \to 0^+$, so $\log_{10}(2 - x) \to -\infty$
• Range: $\mathbb{R}$

3. Prove Logarithmic Properties

Use the definition $\log_b(x) = y \iff b^y = x$ to prove the following properties:

• a) $\log_b(xy) = \log_b(x) + \log_b(y)$
• b) $\log_b(x/y) = \log_b(x) - \log_b(y)$
• c) $\log_b(x^k) = k \log_b(x)$

Solution
a) Prove: $\log_b(xy) = \log_b(x) + \log_b(y)$
Let:

$$\log_b(x) = m \Rightarrow b^m = x \quad \text{and} \quad \log_b(y) = n \Rightarrow b^n = y$$

Multiply:

$$xy = b^m \cdot b^n = b^{m+n} \Rightarrow \log_b(xy) = m + n = \log_b(x) + \log_b(y)$$

b) Prove: $\log_b(x/y) = \log_b(x) - \log_b(y)$
Let $\log_b(x) = m$ and $\log_b(y) = n$

$$\Rightarrow x = b^m, \; y = b^n \Rightarrow \frac{x}{y} = \frac{b^m}{b^n} = b^{m - n} \Rightarrow \log_b(x/y) = m - n = \log_b(x) - \log_b(y)$$

c) Prove: $\log_b(x^k) = k \log_b(x)$
Let $\log_b(x) = m \Rightarrow x = b^m$

$$x^k = (b^m)^k = b^{km} \Rightarrow \log_b(x^k) = km = k \log_b(x)$$

4. Bacteria Growth

A scientist is growing a bacteria culture in a lab. At the start, there are 100 bacteria. The population doubles every 3 hours.

Questions:

• a) Write an exponential function $P(t)$ that models the population after $t$ hours.

• b) How many bacteria will there be after 12 hours?

• c) After how many hours will the population reach at least 6,400 bacteria?

Solution
a) The bacteria doubles every 3 hours starting from 100.
General exponential form:

$$P(t) = P_0 \cdot 2^{t/3}$$

So:

$$P(t) = 100 \cdot 2^{t/3}$$

b) After 12 hours:

$$P(12) = 100 \cdot 2^{12/3} = 100 \cdot 2^4 = 100 \cdot 16 = 1600$$

So, 1600 bacteria after 12 hours.

c) Want:

$$100 \cdot 2^{t/3} \geq 6400 \Rightarrow 2^{t/3} \geq 64 \Rightarrow 2^{t/3} = 2^6 \Rightarrow \frac{t}{3} = 6 \Rightarrow t = 18$$

So, the population reaches at least 6400 after 18 hours.

5. Solve the exponential equation

Solve for $x$:

$$5^{2x} = 5^{x+1} - 6$$

Solution
Solve:

$$5^{2x} = 5^{x+1} - 6$$

Let’s set $y = 5^x$.
Then:

$$5^{2x} = (5^x)^2 = y^2, \quad 5^{x+1} = 5 \cdot 5^x = 5y$$

Substituting:

$$y^2 = 5y - 6 \Rightarrow y^2 - 5y + 6 = 0 \Rightarrow (y - 2)(y - 3) = 0 \Rightarrow y = 2 \text{ or } y = 3$$

Recall $y = 5^x$:

• If $5^x = 2 \Rightarrow x = \log_5(2)$
• If $5^x = 3 \Rightarrow x = \log_5(3)$

Final answers:

$$x = \log_5(2) \quad \text{or} \quad x = \log_5(3)$$

6. Solve the logarithmic equation

Solve for $x$:

$$4 \log_3(x^2) - \log_3(x) = 14$$

Solution
Given:

$$4 \log_3(x^2) - \log_3(x) = 14$$

Use log power rule:

$$\log_3(x^2) = 2 \log_3(x) \Rightarrow 4 \cdot 2 \log_3(x) = 8 \log_3(x)$$

So the equation becomes:

$$8 \log_3(x) - \log_3(x) = 14 \Rightarrow 7 \log_3(x) = 14 \Rightarrow \log_3(x) = 2$$

Now rewrite in exponential form:

$$x = 3^2 = 9$$

Final answer: $x = 9$

Extra Advanced Exercises

1. Exponential and Logarithmic Equation Combo

Solve for ( x ):

$$2^x = 5^{x - 1}$$

2. Domain Puzzle: Log of a Log

Find the domain of:

$$f(x) = \log_2(\log_3(x - 1))$$

3. Change of base formula.

Prove the change of base formula for the log function:

$\log_b(x) = \frac{\log_k(x)}{\log_k(b)}$