lecture 6: Root and Rational Functions — Graphs, Domain and Range, Discontinuities, and Infinity Behavior
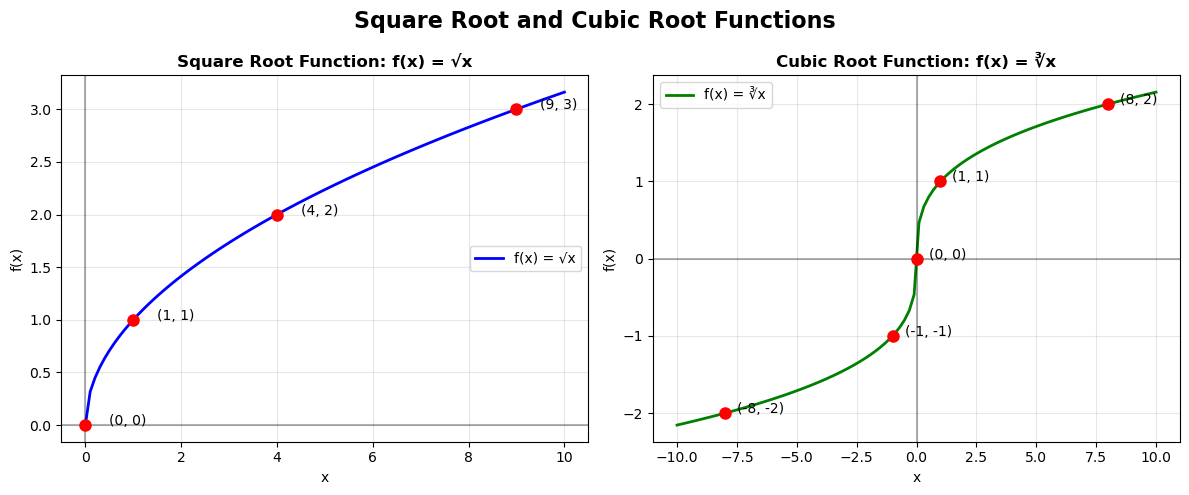
Root Functions
1. What Is a Root Function?
A root function involves square roots, cube roots, or other fractional exponents:
- Square roots only work on non-negative inputs.
- Odd roots (like cube roots) work on all real numbers.
2. Domain and Range
| Function | Domain | Range |
|---|---|---|
Even roots need , odd roots are fine for any .
3. Graphs of Root Functions
- Square Root: starts at (0,0), increases slowly
- Cube Root: passes through (0,0), symmetric across origin
Rational Functions
1. What Is a Rational Function?
A rational function is a ratio of two polynomials:
Examples:
2. Domain and Discontinuity
Rational functions are undefined where the denominator is zero.
Example:
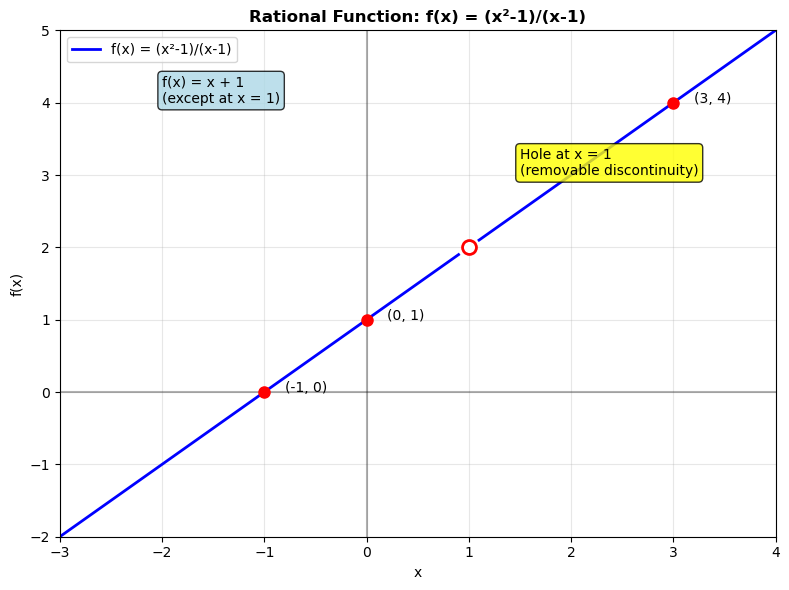
3. Types of Discontinuities
a) Removable (a "hole"):
Happens when a factor cancels from top and bottom.
Hole at
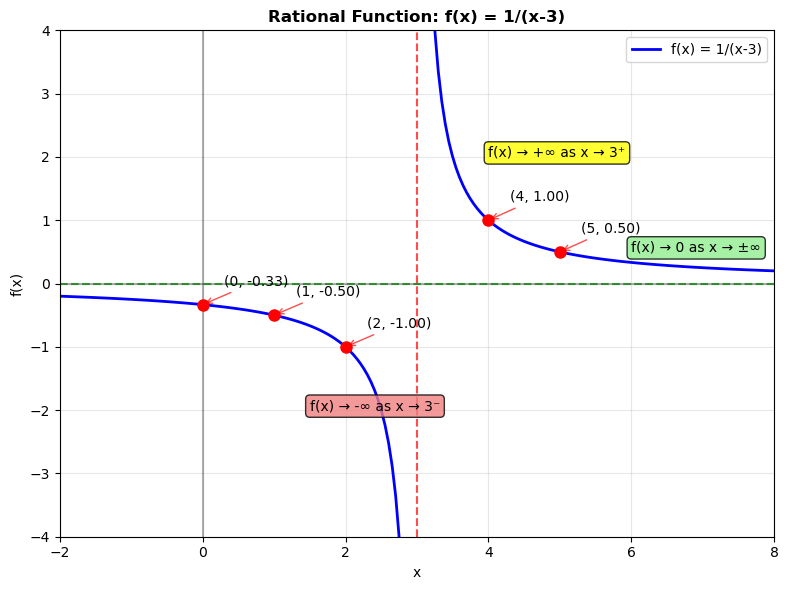
b) Essential (vertical asymptote):
Occurs when the denominator goes to zero and does not cancel.
Asymptotes and Graph Behavior
1. Vertical Asymptotes
- Occur where the denominator = 0 and does not cancel.
2. Horizontal & Slant Asymptotes
| Degree Comparison (Top vs Bottom) | Asymptotic Behavior |
|---|---|
| Degree top < bottom | Horizontal at |
| Degree top = bottom | Horizontal at |
| Degree top > bottom | Slant asymptote (do long division) |
3. Examples
Example 1:
Left side:
Domain:
Vertical asymptote:
Oblique asymptote:Right side:
Domain:
No vertical asymptotes
Oblique asymptote: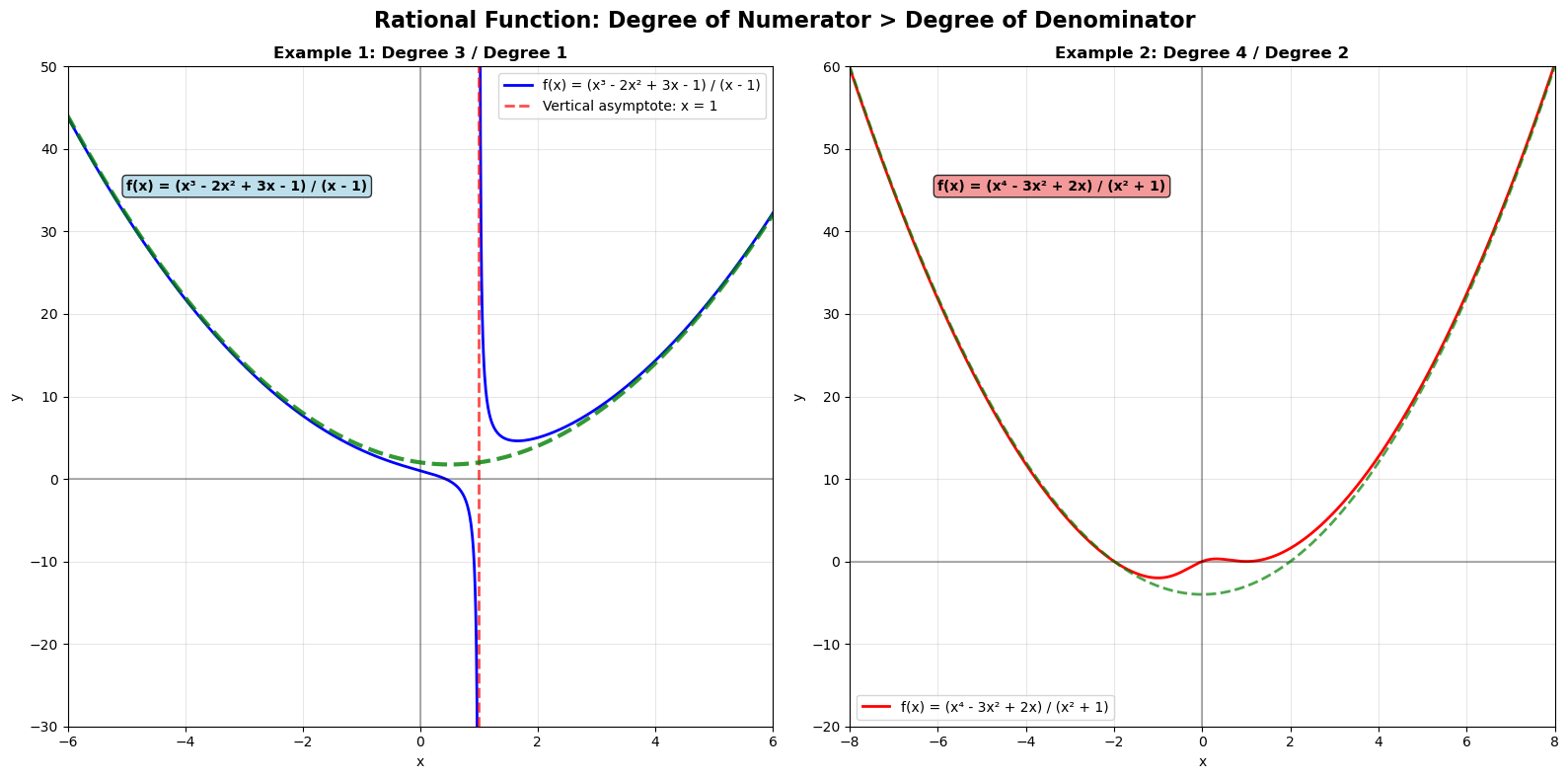
Example 2:
Domain:
Vertical asymptotes:
Horizontal asymptote: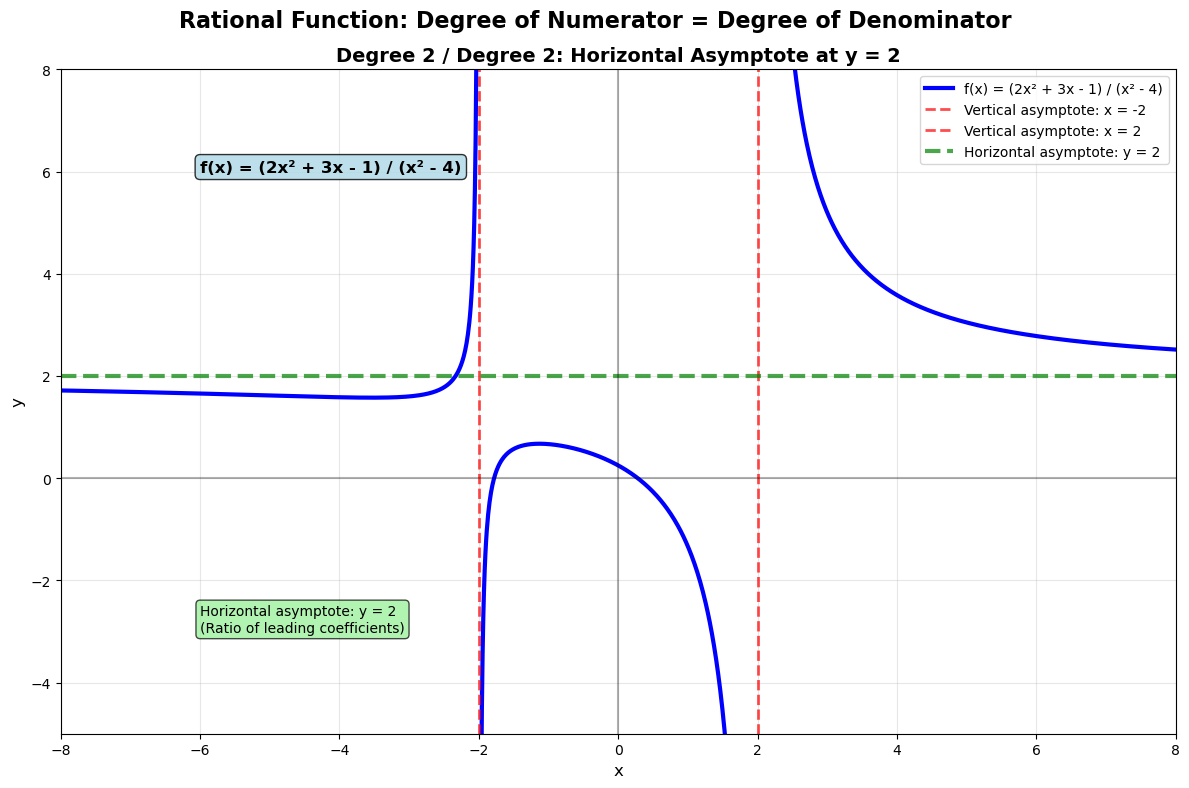
Infinity Behavior
Root Functions
- As , root functions grow — but slowly.
- as , as
Rational Functions
- As , rational functions approach asymptotes (if they exist).
- e.g.,
Regular Exercises
1. Graph Analysis
Study the graph below and answer the questions about this rational function:
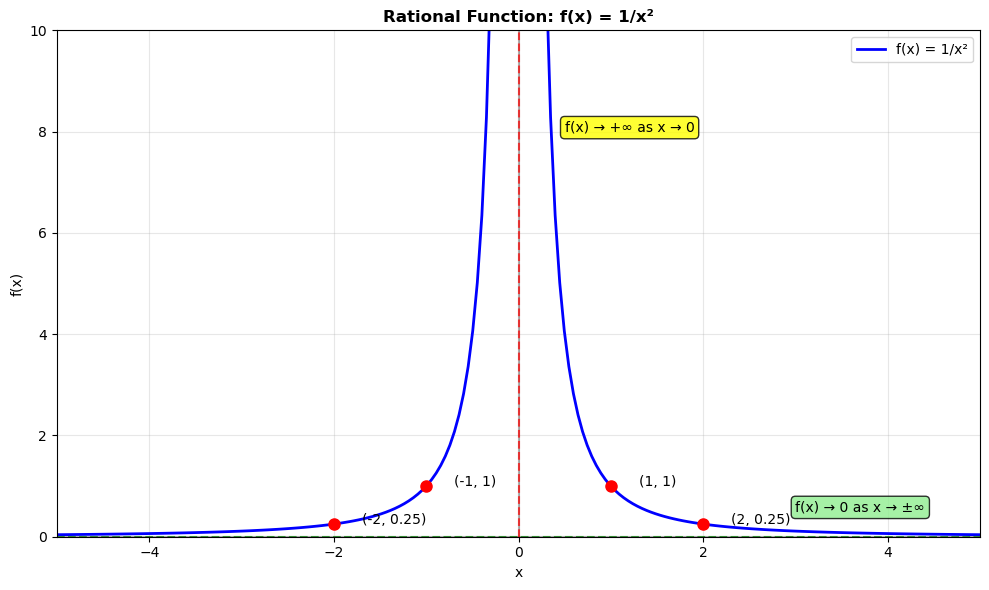
a) What is the domain of this function?
b) What type of discontinuity occurs at x = 0?
c) What is the horizontal asymptote of this function?
write your answer in the form y=... with no spaces
d) What is the range of this function?
e) As x approaches 0 from the right, what happens to f(x)?
f) As x approaches 0 from the left, what happens to f(x)?
2. Types of Discontinuity
Determine whether the discontinuity is removable or essential:
-
a)
-
b)
-
c)
3. Domain and Discontinuity
Find the domain of each function and describe any discontinuities:
- a)
- b)
- c)
Solution
a)
- A square root is only defined when the expression inside is ≥ 0.
- So:
- Domain:
- Discontinuity: None; the function is continuous for all values in its domain.
b)
- Denominator cannot be zero:
- Domain:
- Discontinuity: Vertical asymptotes at
c)
- Factor numerator:
- The ( x - 2 ) cancels, leaving , but the original function is undefined at ( x = 2 ).
- Domain:
- Discontinuity: Removable discontinuity (hole) at ( x = 2 )
4. Root Domain Puzzle
For each function, find the domain, but without graphing. Justify your reasoning algebraically:
- a)
- b)
- c)
Solution
a)
- Inside square root must be ≥ 0:
- Domain: ( [-2, 2] )
b)
- Square root is defined when:
- Domain:
c)
- Find where the expression is ≥ 0. Use sign chart:
- Critical points: ( x = -2 ) and ( x = 1 )
- Test intervals:
- ( x < -2 ): both factors negative → product positive
- ( -2 < x < 1 ): one factor negative → product negative
- ( x > 1 ): both positive → product positive
- Include points where the expression = 0
- Domain:
5. Impossible Graph?
Here is a graph sketch:
-
It has a hole at
-
It has a vertical asymptote at
-
It has a horizontal asymptote at
- a) Can you write a rational function that fits this behavior?
- c) What happens if you remove the factor that causes the hole?
Solution
a) We need a rational function with:
- Hole at ( x = 2 ): this means the factor ( (x - 2) ) is canceled
- Vertical asymptote at ( x = -1 ): the factor ( (x + 1) ) is in the denominator but not canceled
- Horizontal asymptote at ( y = 3 ): degree of numerator = degree of denominator; leading coefficients ratio = 3
One possible function:
- Hole at ( x = 2 ), vertical asymptote at ( x = -1 ), and horizontal asymptote at ( y = 3 ) ✔️
b) If we remove the factor that causes the hole (i.e., cancel ( (x - 2) ) from numerator and denominator), the hole disappears.
The function becomes:
Now it is defined at and is no longer discontinuous there.
6. Graph from Clues
Build a rational function that:
-
Has a vertical asymptote at
-
Has a hole at
-
Has a horizontal asymptote at
-
Crosses the x-axis at
- a) Write a possible expression.
- b) Label all key features on a sketch.
- c) Change your function so that the horizontal asymptote is now . What did you change?
Solution
a) Features needed:
- Vertical asymptote at ( x = 2 ): means factor ( (x - 2) ) in denominator
- Hole at ( x = -1 ): means factor ( (x + 1) ) in both numerator and denominator
- Horizontal asymptote at ( y = 1 ): numerator and denominator same degree; leading coefficients equal
- Zero at ( x = 3 ): factor ( (x - 3) ) in numerator
A possible function:
- The ( (x + 1) ) cancels, creating a hole at ( x = -1 )
b) Key features on the graph:
- Hole at ( x = -1 )
- Vertical asymptote at ( x = 2 )
- x-intercept at ( x = 3 )
- Horizontal asymptote at ( y = 1 ) (degrees equal, leading coefficients = 1)
c) To change the horizontal asymptote to ( y = 5 ), make the leading coefficient of the numerator 5:
After canceling, this becomes:
Now the degrees are still equal, but the ratio of leading coefficients is 5, so the horizontal asymptote is ( y = 5 ).
Extra Advanced Exercises:
1. Asymptotic Limit Puzzle
Let
- a) Find the limit as using rationalization
- b) Does this function have a horizontal asymptote?
- c) Analyze symmetry and behavior as
2. Rational Function with Parameters
Let
- a) Find conditions on ( a ) and ( b ) such that:
- The function has no x-intercepts
- A vertical asymptote at ( x = 2 )
- A horizontal asymptote at ( y = 1 )
- b) Based on those conditions, determine the range of ( f(x) )
3. Domain and Discontinuity of a Root-Rational Combo
Let
- a) Determine the domain algebraically
- b) Identify and classify all discontinuities
- c) Analyze end behavior as