lecture 5: Polynomial functions, their graphs, their domain and range, and their infinity behavior
What Are Polynomial Functions?
1. Real-World Motivation
Polynomials help model real-life situations with more complexity than just straight lines or parabolas.
Examples include:
- Profit modeling:
- Population changes with limits or crashes
- Motion under forces (e.g., with acceleration, friction)
A polynomial is a function made by adding powers of with constant coefficients:
Where:
- is a non-negative integer (the degree)
- The values are real numbers
Why Study Polynomials?
- They are defined everywhere (no gaps or breaks)
- Easy to compute and graph
- Used as approximations in calculus (Taylor polynomials)
- Their graphs are smooth and continuous
- Appear in physics, engineering, economics, and more
Domain and Range
1. Domain
All polynomials are defined for all real numbers.
2. Range
The range depends on:
- The degree (odd or even)
- The leading coefficient
We usually estimate range using the graph or calculus (later in the course).
Roots of Polynomials
1. What are Roots?
A root of a polynomial is a value of that makes the polynomial equal to zero.
2. How to find roots?
- Factoring: If , then are the roots.
- Quadratic formula: For , the roots are .
- Synthetic division: If , then is a root. Then, for some polynomial .
3. Example
Let:
- Roots:
- Factored form:
Graphing Polynomial Functions
1. Shape and Degree
The degree of a polynomial controls how many “turns” the graph can have.
| Degree | Common Shape | Max Turning Points |
|---|---|---|
| 1 | Line | 0 |
| 2 | Parabola | 1 |
| 3 | S-shaped | 2 |
| 4 | W- or M-shaped | 3 |
Example of polynomials of different degrees:
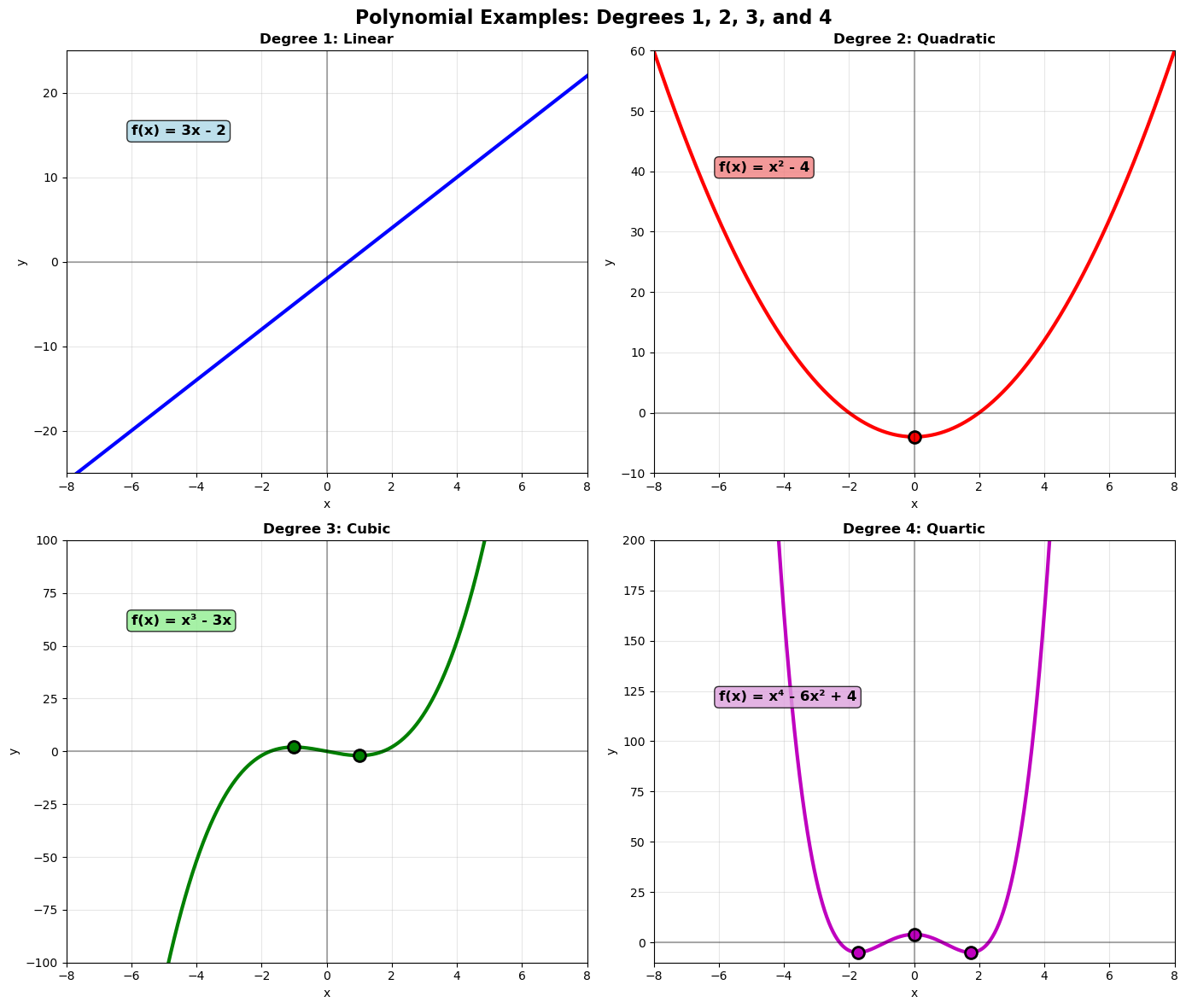
A degree- polynomial has at most turning points.
2. Infinity Behavior (a.k.a. End Behavior)
As , the graph of the polynomial behaves like its leading term.
| Degree | Leading Coefficient | End Behavior |
|---|---|---|
| Even | Positive | as |
| Even | Negative | as |
| Odd | Positive | as , as |
| Odd | Negative | as , as |
An infographic picture of polynomials behaviour at infinities:

Example with functions:
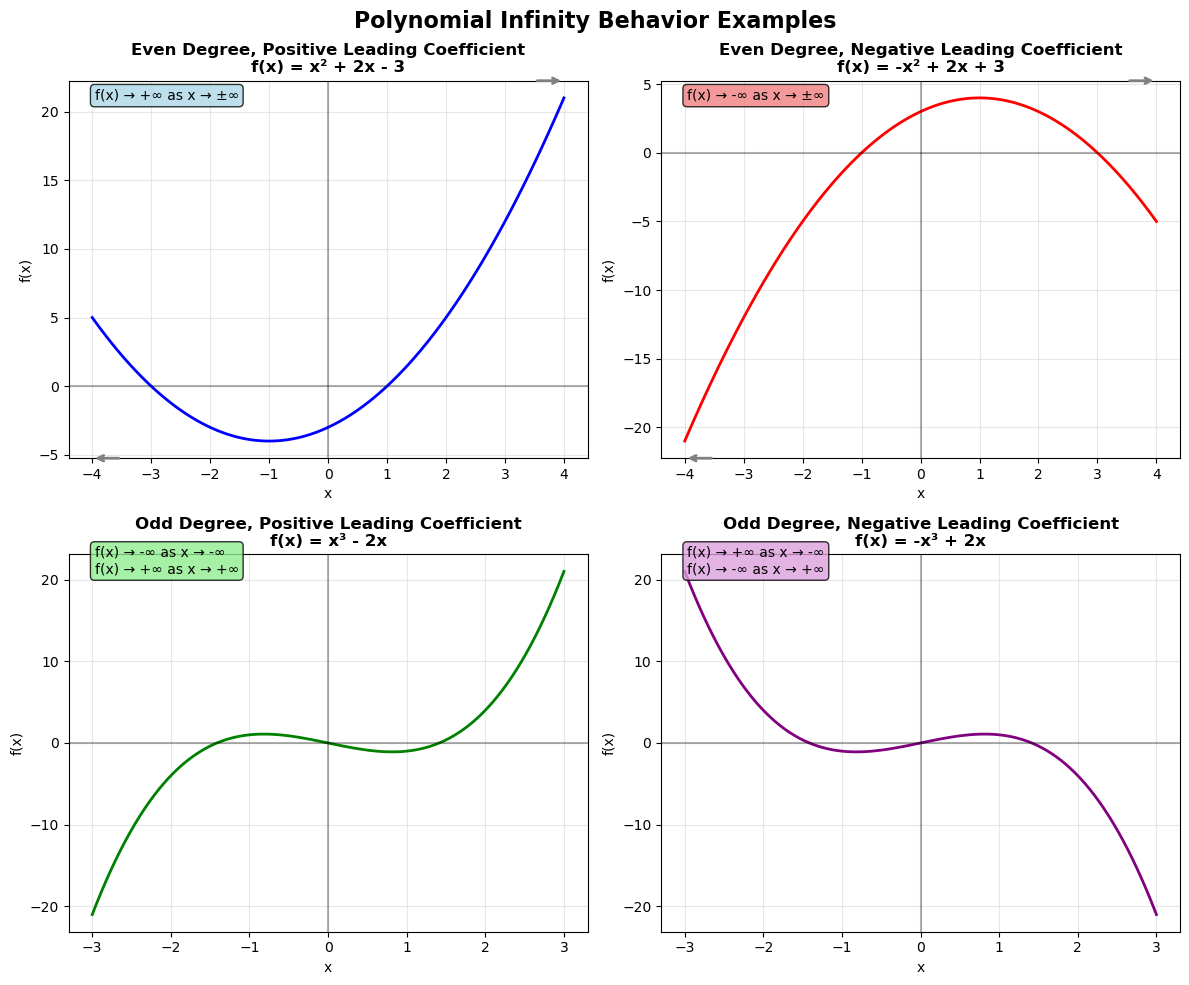
3. Example
Let:
- Degree: 3 (cubic)
- Leading coefficient: 1 (positive)
- Domain:
- Range: (since degree is odd)
Turning Points: Up to 2
End Behavior:
as
as
Regular Exercises
1. Classify Polynomials
For each function, write the degree, leading coefficient, and whether it has an absolute maximum or minimum:
-
a)
-
b)
-
c)
2. Match the Graph to the Function
Each of the following is a sketch of a polynomial. Without using a calculator:
- Decide if the degree is odd or even
- Determine if the leading coefficient is positive or negative
- Predict how many turning points it might have
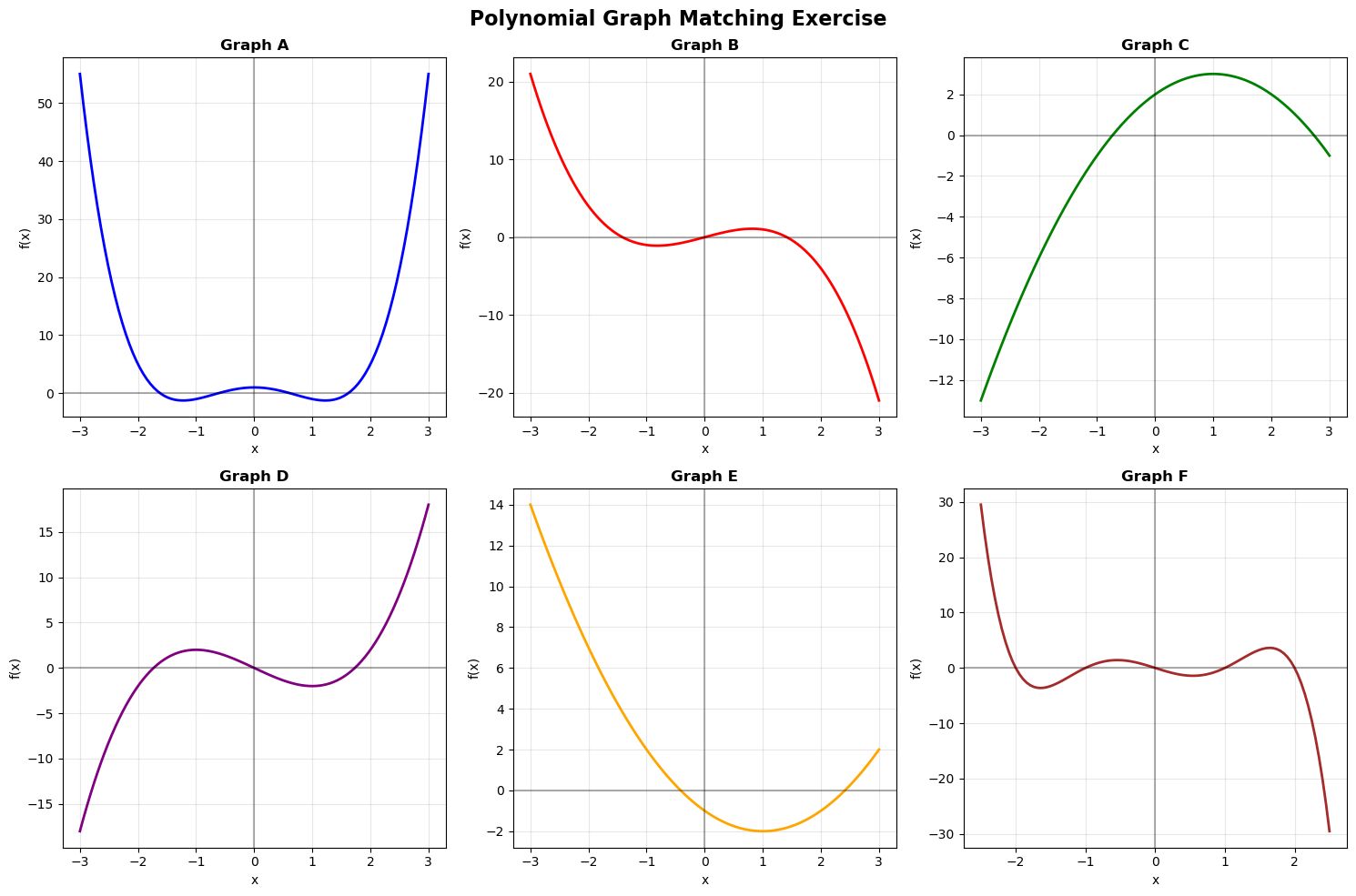
-
Graph A:
-
Graph B:
-
Graph C:
-
Graph D:
-
Graph E:
-
Graph F:
3. Real-World Modeling
A company's profit over time is modeled by:
- a) What is the degree of this polynomial?
- b) What does the negative leading coefficient tell you about its long-term behavior?
- c) When might the company be losing money? (Estimate from the graph or table of values)
Solution
a) The function is:
The degree of a polynomial is the highest power of the variable. Here, the highest power is , so the degree is:
Degree = 3b) The leading coefficient is the coefficient of the highest degree term, which is −2.
Since it is negative and the degree is odd, the graph will rise to the left and fall to the right.
In other words, as ,
and as ,This means that in the long run, the company's profits will decrease (possibly losses grow).
c) The company is losing money when .
Without graphing exactly, we can estimate by plugging in a few values:
So the company begins losing money around and continues downward afterward.
4. Design a Polynomial
Create a polynomial function that meets all of the following conditions:
-
Degree = 3
-
Positive leading coefficient
-
Passes through the origin:
-
Has a turning point somewhere between and
- a) Write a possible formula.
- b) Sketch a rough graph.
- c) What is the domain and range?
Solution
a) We want a degree 3 polynomial, with positive leading coefficient, that passes through the origin (), and has a turning point between and .One possible function is:
- Degree = 3 ✔️
- Leading coefficient = 1 (positive) ✔️
- ✔️
- Turning points occur near ✔️
c)
- Domain: All real numbers,
- Range: All real numbers, (since cubic polynomials have no upper/lower bounds)
5. Polynomial Passing Through Points
You are told a cubic polynomial passes through the following points:
-
-
-
-
-
a) Write a possible formula for in factored form.
-
b) Expand the expression into standard form.
-
c) What is the leading coefficient and what does it tell you about end behavior?
-
d) What is the domain and range of your function?
Solution
a) We're told the function is cubic and passes through three x-intercepts (three roots):
, , , andThis suggests we can write the function in factored form:
Use to solve for :
So, the function is:
b) Expand the expression:
First expand two of the factors:
Multiply with the third:
Multiply by :
c) The leading coefficient is −2
- Since the degree is 3 (odd) and the leading coefficient is negative, the end behavior is:
- ,
- ,
This tells us the function falls to the right and rises to the left.
d)
- Domain: All real numbers,
- Range: All real numbers, (cubic polynomials are unbounded vertically)
Extra Advanced Exercises
1. Multiplicity Investigation
Consider the polynomial .
- a) How many real roots does this polynomial have?
- b) At which -values does the graph of cross the -axis?
2. Turning Points Estimation
Suppose
- a) Find the x-intercepts of the graph of .
- b) Use symmetry and reasoning to estimate the turning points of the graph.
- c) What is the maximum value of ?
3. Difference of polynomials
Let .
- a) Compute .
- b) What is the degree of the polynomial in part (a)?
Consider the polynomial .
- c) What is the degree of the polynomial ?