lecture 4: Formal definition of a function, simple examples of functions (linear, quadratic), how to draw them and how to figure out their domain and range.

What is a function?

1. Motivational Real-World Example

Vending Machine Analogy:
A vending machine takes in a selection code (e.g., A1, B2) and gives you a unique snack. If you press A1, you always get the same item. It doesn't give two snacks, and it doesn't give you different items each time.
That’s the essence of a function: Each input leads to exactly one output.

2. Formal Definition

A function is a rule that assigns each element from a set called the domain to exactly one element in another set called the range.

Notation:
$f:A\to B$, where $f(x) \in B$ for each $x \in A$.
($A$ is the domain and $B$ is the range.)

3. Domain and Range

• Domain: All the inputs $x$ for which the function is defined.
• Range: All possible outputs $f(x)$ the function can produce.

Two functions can have the same domain and range but be completely different rules.
(e.g., $f(x)=x$ vs. $g(x)=−x$).

Co-domain vs. Range

• Co-domain: The set of all possible outputs that could be produced by the function.
• Range: The set of all actual outputs that are produced by the function.

So, the range is a subset of the co-domain.

Example:
$f(x)=x^2$

• Co-domain: all real numbers
• Range: all non-negative real numbers

4. Why Do We Care?

• Functions are how we model relationships between quantities: position vs. time, cost vs. production, temperature vs. altitude.

• In calculus, functions are the primary objects of study for understanding change and motion.

5. Examples

• A temperature converter: $F = \frac{9}{5}C + 32$
• A vending machine: $f(\text{button}, \text{money}) = \text{snack}$
• A calculator: pressing "=" gives you the result of the expression you entered.
  • This is a function because each input (expression) gives exactly one output (result).

Examples of mappings that are not functions:

• Person to their phone number: a person can have multiple phone numbers.
• Restaurant menu special: a special can change every day.
• Birthday to person: same birthday maps to multiple people.
• Language translation: same word can have multiple meanings.

Questions:

• Is ChatGPT a function?
• Is Google search a function?

Linear Functions

1. Example

If you earn 10 Riyals for every hour worked: $y=10x$ is a linear function.

2. General Form

$$f(x)=mx+b$$

• m = slope (rate of change)
• b = y-intercept (starting value)

3. Graph

• Always a straight line.
• Slope = rise/run.
• Domain = all real numbers ($\mathbb{R}$)
• Range = all real numbers ($\mathbb{R}$)

Example:
Graph of 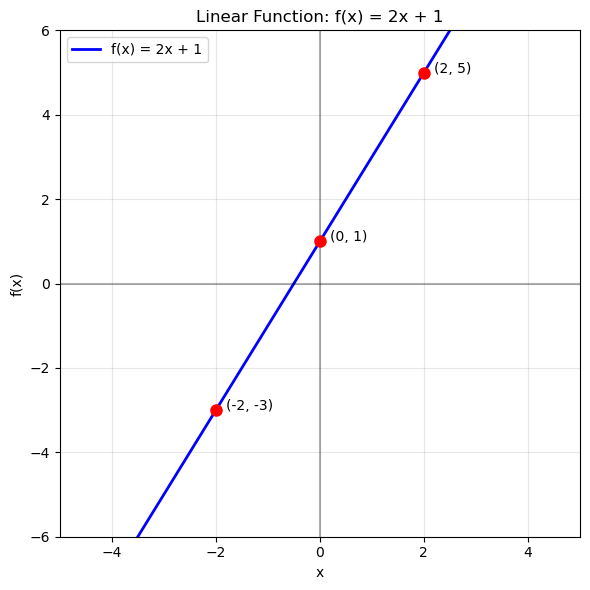$f(x)=2x+1$:

Quadratic Functions

1. Why Use Quadratics?

Used to model things like:

• Projectile motion
• Revenue as a function of sales
• Area as a function of side length

2. General Form

$$f(x)=ax^2+bx+c$$

• Parabolic shape (opens up if $a>0$, down if $a<0$)
• Vertex is turning point

3. Domain and Range

• Domain: $\mathbb{R}$
• Range:
  • If $a>0$, $[\text{min},\infty)$
  • If $a<0$, $(−\infty,\text{max}]$

Example:
Graph of $f(x)=x^2−2x+1$

• Domain: all real numbers
• Range: depends on the minimum point. In this case, the minimum point is at $y=0$.

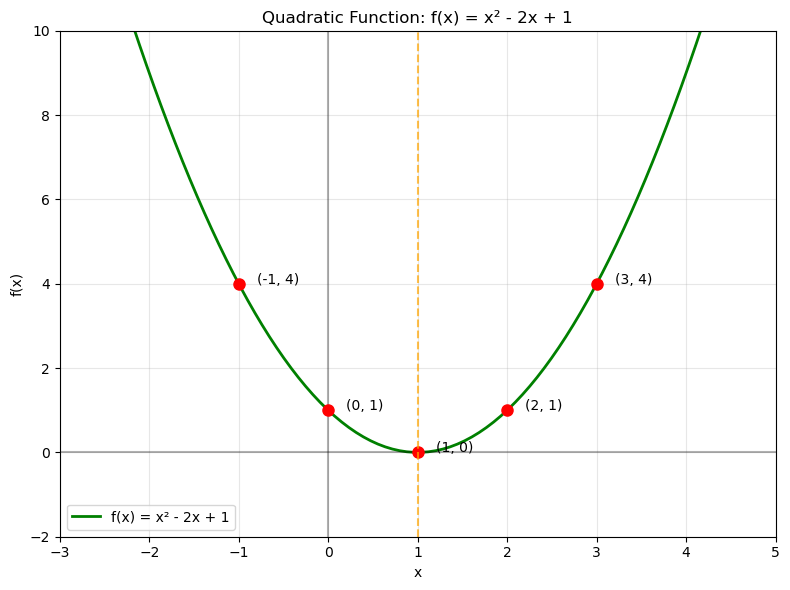
4. Vertex

The vertex of a quadratic function is the point where the function changes direction.

The x-coordinate of the vertex of a quadratic function $f(x)=ax^2+bx+c$ is given by the formula:

$$x=-\frac{b}{2a}$$

The y-coordinate of the vertex is then found by plugging the x-coordinate back into the function.

Example:
$f(x)=x^2-2x+1$

• The x-coordinate of the vertex is $x=-\frac{-2}{2(1)}=1$.
• The y-coordinate of the vertex is $f(1)=1^2-2(1)+1=0$.
• The vertex is at $(1,0)$.

Function evaluation

If given a formula, function evaluated at a point is the value of the function at that point.

Examples:

• $f(x)=x^2+2x+1$
  • $f(-1)=(-1)^2+2(-1)+1=0$
• $g(x)=2^{x+3}$
  • $g(2)=2^{2+3}=2^5=32$

By the same logic, we can evaluate functions at points represented by expressions.

Examples:

• $f(x)=x^2+2x+1$
  • $f(-x)=(-x)^2+2(-x)+1=x^2-2x+1$
  • $f(2y)=(2y)^2+2(2y)+1=4y^2+4y+1$
  • $f(x+1)=(x+1)^2+2(x+1)+1=x^2+2x+1+2x+2+1=x^2+4x+4$

Regular Exercises

1. Water Tank Domain and Range

A water tank is being drained. The function $h(t)$ gives the amount of water (in liters) left in the tank after $t$ minutes.
The tank starts full at 100 liters, and drains at 5 liters per minute, until empty.

• a) Write a possible rule for $h(t)$.
• b) What is the domain of $h(t)$?
• c) What is the range of $h(t)$?
• d) Could this function continue forever?

Solution
a) The tank starts full at 100 liters and drains at a rate of 5 liters per minute. Once it’s empty, the amount of water stays at 0.

A piecewise function to represent this is:

$$h(t) = \begin{cases} 100 - 5t & \text{if } 0 \leq t \leq 20 \\ 0 & \text{if } t > 20 \end{cases}$$

b) The domain is all non-negative real numbers since time can continue indefinitely:

$$\text{Domain: } [0, \infty)$$

c) The range is all the possible values of $h(t)$. The tank drains from 100 liters to 0 and stays at 0:

$$\text{Range: } [0, 100]$$

d) Yes, the function continues forever. After 20 minutes, the tank is empty and the water level remains at 0 for all $t > 20$.

2. Photo Frame

You have a square photo print with side length $x$ centimeters. You want to add a frame of constant width $2$ centimeters all around it.

• Suppose you have exactly $100 \text{ cm}^2$ of frame material available.
  • Write and solve an equation to find the side length of the photo that would exactly use up the available frame material.

Hint: Write the area of the frame as a function of $x$, and then solve for $x$.

Solution
Let the photo side length be $x$ cm. The frame adds 2 cm all around, so the total side length with frame is:

$$x + 2 + 2 = x + 4$$

The area of the photo alone is:

$$x^2$$

The area of the photo plus frame is:

$$(x + 4)^2$$

The area of the frame alone is the difference:

$$\text{Frame area} = (x + 4)^2 - x^2$$

Given frame area = 100 cm², write the equation:

$$(x + 4)^2 - x^2 = 100$$

Expand:

$$x^2 + 8x + 16 - x^2 = 100 \implies 8x + 16 = 100$$

Solve for $x$:

$$8x = 84 \implies x = 10.5$$

So, the photo side length should be 10.5 cm.

3. Quadratic Function Construction

Construct a quadratic function $f(x)$ that satisfies the following:

• The vertex is at $(2,−3)$
• $f(0)=5$

Solution
The vertex form of a quadratic is:

$$f(x) = a(x - h)^2 + k$$

where vertex is at $(h,k)$. Here, vertex $(2,-3)$ gives:

$$f(x) = a(x - 2)^2 - 3$$

Use $f(0) = 5$ to find $a$:

$$5 = a(0 - 2)^2 - 3 \implies 5 = 4a - 3$$

$$4a = 8 \implies a = 2$$

Therefore, the function is:

$$f(x) = 2(x - 2)^2 - 3$$

4. Reverse Engineering a Function

You are given that:

• $f(0)=2$

• $f(1)=5$

• $f(2)=8$

• $f(3)=11$

  • a) Can you guess a formula for $f(x)$?
  • b) Is your function linear or nonlinear? How can you tell?
  • c) Could more than one rule produce these values? Why or why not?

Solution
a) Look at the values:

$$\begin{aligned} f(0) &= 2 \\ f(1) &= 5 \\ f(2) &= 8 \\ f(3) &= 11 \end{aligned}$$

Notice that each time $x$ increases by 1, $f(x)$ increases by 3. So the function increases linearly with slope 3.
A possible formula is:

$$f(x) = 3x + 2$$

b) The function is linear because the output changes by a constant amount (3) for every increase of 1 in $x$.

c) Could more than one rule produce these values?
Technically, yes — more than one function could match these four points but behave differently elsewhere.

For example, consider the absolute value function:

$$f(x) = 3|x - 1| + 2$$

Let's check the values:

$$\begin{aligned} f(0) &= 3|0 - 1| + 2 = 3(1) + 2 = 5 \\ f(1) &= 3|1 - 1| + 2 = 0 + 2 = 2 \\ f(2) &= 3|2 - 1| + 2 = 3(1) + 2 = 5 \\ f(3) &= 3|3 - 1| + 2 = 3(2) + 2 = 8 \end{aligned}$$

These outputs do not match the original $f(x)$ values, proving this is a different rule. However, with careful design, a nonlinear function could be made to match specific points.

This example shows that just a few input-output pairs aren’t enough to uniquely determine a function, especially if you're not assuming linearity. Different rules can fit the same values at some $x$ but behave differently elsewhere.

Extra Advanced Exercises

1. Fencing a Rectangular Area

You are given 40 meters of fencing and want to enclose a rectangular area against a wall (so you only need to fence three sides). Let $x$ be the width of the fenced rectangle.

• a) Write a function $A(x)$ for the area in terms of $x$.
• b) What is the domain of $A(x)$?
• c) Find the value of $x$ that gives the maximum area, and explain how you know it's a maximum.

2. Composing Functions

You’re told that:

$$h(x)=\sqrt{2x+3}$$

And someone tells you it came from composing two functions $f$ and $g$, so that
$h(x)=f(g(x))$

• a) Find at least one possible pair $(f,g)$ such that this is true.
• b) Can you find a different pair of functions that also work?
• c) What is the domain of $h(x)$? How does that relate to the domains of $f$ and $g$?